منظور از ریشهها یک تابع مقادیری برای متغیرهای ورودی آن هستند که به ازای آنها خروجی تابع صفر شود. به عنوان مثال خروجی تابع $f(x)=2x-4$ به ازای $x=2$ صفر یا مقدار $2$ ریشه معادله $2x-4=0$ است. به همین ترتیب در مورد معادلات درجه دوم نیز میدانیم چطور میتوانیم به ریشه یا ریشهها در صورت موجود بودن دست پیدا کنیم. البته لزومی ندارد پاسخ معادله یک عدد صحیح یا گویای متناهی باشد. به عنوان مثل جواب معادلههای $x^2 - 2 = 0$ و $sin(\frac{x}{2}) = 1$ به ترتیب اعداد گنگ $\sqrt{2}$ و $\pi$ هستند که در عمل امکان ذخیرهسازی تک تک ارقام اعشاری در کامپیوتر وجود ندارد.
مسائل دنیای واقعی اغلب پیچیده بوده و به سادگی با روشهای تحلیلی حل نمیشوند. به ویژه آنکه معمولا وابسته به تنها یک متغیر نیستند. به عنوان یک نمونه ساده معادلات درجه سوم و بالاتر علیرغم تک متغیره بودن راه حل قطعی ندارند. از سوی دیگر قدرت عملیاتی انسان در علوم مختلف در ایدهآلترین حالت در مقیاس نانو صورت میگیرد که دقت عدد در حد ۹ رقم اعشار اهمیت پیدا میکند و این یعنی در اختیار داشتن رفتم بیستم اعشار $\sqrt{2}$ عموما چندان کارکرد عملی ندارد و از حل معادلهی $x^2 - 2 = 0$ در نهایت ۹ یا ۱۲ رقم اعشار قابل استفاده است.
منظور از روشهای عددی (یا روشهای تقریب) برای حل یک معادله حرکت به سمت ریشه با استفاده از یک الگوریتم تکرارشونده تا زمان رسیدن به خود ریشه یا دقت مطلوبی از آن است. اگر اعداد تولید شده در این تکرارها را به صورت دنباله $\{x_n\}$ نمایش دهیم، حد این دنباله به یک ریشه تابع (در صورت وجود) همگراست. برای آنکه بتوانیم به صورت گام به گام به ریشه نزدیک شویم در وهله اول باید بازهای پیدا کنیم که مطمئن باشیم حتما در آن بازه ریشه وجود دارد. ثابت میشود (قضیه مقدار میانی) اگر تابع در یک بازه پیوسته و مقدار آن به ازای دو نقطه شروع و پایان علامت مختلف داشته باشد (یعنی $ f(a)f(b)<0 $)، حتما در آن بازه حداقل یک ریشه وجود دارد. بدیهی است اگر تابع در این بازه اکیدا نزولی یا اکیدا صعودی باشد تنها یک ریشه وجود خواهد داشت (چرا؟).
در شرایطی که رسیدن به عدد دقیق ریشه مد نظر یا ممکن نباشد، با یکی از شرطهای زیر میتوان تکرار الگوریتم ریشهیابی را متوقف کرد.
-
کوچکتر کردن بازه مورد جستجو تا زمانی که اختلاف دو سر آن کمتر از حد مطلوبی شود. به عنوان مثال اگر اختلاف دو سر بازه کمتر از $0.001$ باشد سه رقم اول اعشار هر عددی در آن بازه یک مقدار است و میتوان آن عدد را به عنوان ریشه با دقت سه رقم اعشار در نظر گرفت. در واقع رویکرد کلی این روشها استفاده از تکنیک
تقسیم و حل برای نزدیک شدن به ریشه معادله است.
-
مقدار $ |f(x_i)| $ کمتر از حد مطلوبی شود.
-
مقدار $ |x_i - x_{i-1}| $ کمتر از حد مطلوبی شود.
-
تعداد تکرار الگوریتم به کرانه مشخص شده برسد.
در ادامه با چند الگوریتم مشهور ریشهیابی آشنا میشویم.
الگوریتم ریشهیابی تنصیف
[برگرد بالا]
الگوریتم تنصیف (روش دو بخشی) برای تابع دلخواه $f$ در بازه $a$ تا $b$ و میزان خطای قابل قبول $e$ شامل مراحل زیر است.
-
شروع
-
مقدار $\frac{a+b}{2}$ را در $m$ قرار بده.
-
اگر اختلاف $a$ و $b$ کمتر از $e$ یا $f(m)$ برابر صفر است برو به مرحله ۷.
-
اگر حاصلضرب $f(a)$ و $f(m)$ منفی بود $m$ را در $b$ قرار بده.
-
اگر حاصلضرب $f(b)$ و $f(m)$ منفی بود $m$ را در $a$ قرار بده.
-
برو به مرحله ۲.
-
مقدار $m$ صفر تابع با دقت $e$ است.
-
پایان
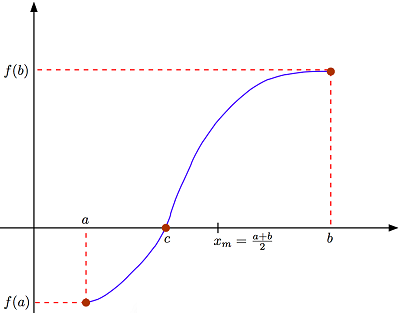
این الگوریتم مشابه الگوریتم جستجوی دودویی در فضای گسسته برای آرایههای مرتب است و پس از محاسبه وسط بازه در متغیر $m$ یکی از دو بازه $a$ تا $m$ یا $m$ تا $b$ را در تکرار بعدی استفاده میکند. بنابراین همانطور که در آن الگوریتم آرایه باید مرتب باشد، شرط عملکرد درست الگوریتم تنصیف نیز یکنوای اکید بودن (صفر نبودن مشتق) در بازه است. اما بر خلاف الگوریتم جستجوی دودویی این روش چندان کارا نیست و سرعت همگرایی کمی دارد. قطعه کد زیر یک نمونه پیادهسازی الگوریتم ریشهیابی تنصیف با زبان برنامهنویسی پایتون است.
def bisection(f: "function", start: float, end: float, e: float, maxIteration : int):
it = 0
while True:
m = (start + end) / 2
if f(m) == 0 or end - start < e or it == maxIteration:
break
if f(start) * f(m) < 0:
end = m
else:
start = m
it += 1
return m
الگوریتم ریشهیابی نیوتن-رافسون
[برگرد بالا]
روش ریشهیابی نیوتن-رافسون که به آن الگوریتم ریشهیابی مماس نیز گفته میشود از مشتق تابع برای رسیدن سریعتر به دقت مورد نظر استفاده میکند. پیشنیاز استفاده از این الگوریتم صفر نبودن مشتق تابع در نقاط بازه و عدم تغییر علامت مشتق دوم در آن بازه است. در چنین شرایطی اگر $x_0$ یک تقریب اولیه از صفر تابع در بازه $a$ تا $b$ باشد، دنباله $x_n$ به صفر تابع همگرا خواهد بود.
$x_n = x_{n–1}- \frac{f(x_{n-1})}{f\prime(x_{n–1})}$
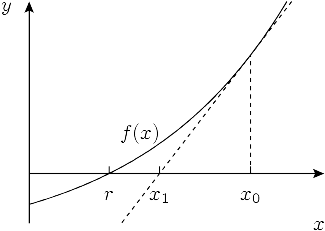
قطعه کد زیر یک نمونه پیادهسازی الگوریتم ریشهیابی نیوتن-رافسون با زبان برنامهنویسی پایتون است.
def newton_1(f: "function", df : "function", x0: float, e: float, maxIteration : int):
it = 0
while True:
x = x0 - f(x0) / df(x0)
if abs(f(x)) < e or it == maxIteration:
break
x0 = x
it += 1
return x
در این پیادهسازی علاوه بر تابع $f$ تابع $df$ نیز به عنوان مشتق تابع دریافت میشود. اما در صورت نیاز میتوان مشتق دقیق تابع در یک نقطه را با شیب خط واصل آن با یک نقطه نزدیکش جایگزین کرد:
def newton_2(f: "function", x0: float, e: float, maxIteration : int):
it = 0
df = lambda x: (f(x + 1e-6) - f(x)) / 1e-6
while True:
x = x0 - f(x0) / df(x0)
if abs(f(x)) < e or it == maxIteration:
break
x0 = x
it += 1
return x
الگوریتم ریشهیابی نیوتن-رافسون همگرایی بسیار سریعتر در مقایسه با الگوریتم ریشهیابی تنصیف دارد، اما وابسته به انتخاب مقدار $x_0$ است. اگر $x_0$ به درستی انتخاب نشود ممکن است دنباله اعداد هرگز به ریشه همگرا نشود.
الگوریتم ریشهیابی نابجایی
[برگرد بالا]
الگوریتم ریشهیابی نابجایی (روش براکت) را میتوان نوعی ترکیب الگوریتمهای نصف کردن و نیوتن-رافسون دانست. این روش مشابه روش نصف کردن از قطعهبندی بازه برای رسیدن به ریشه و مانند روش نیوتن-رافسون از محل تقاطع خطوط با محور طولها برای انتخاب نقطه جدید استفاده میکند. الگوریتم ریشهیابی نابجایی برای تابع دلخواه $f$ در بازه $a$ تا $b$ و میزان خطای قابل قبول $e$ شامل مراحل زیر است.
-
شروع
-
مقدار $a – f(a) \frac{b-a}{f(b)-f(a)}$ را در $m$ قرار بده.
-
اگر اختلاف $a$ و $b$ کمتر از $e$ یا $f(m)$ برابر صفر است برو به مرحله ۷.
-
اگر حاصلضرب $f(a)$ و $f(m)$ منفی بود $c$ را در $b$ قرار بده.
-
اگر حاصلضرب $f(b)$ و $f(m)$ منفی بود $c$ را در $a$ قرار بده.
-
برو به مرحله ۲.
-
مقدار $m$ صفر تابع با دقت $e$ است.
-
پایان
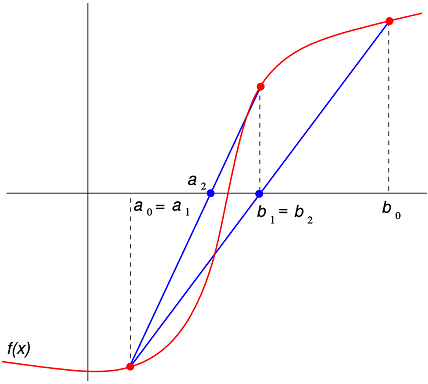
تنها اختلاف این الگوریتم با الگوریتم تنصیف در روش محاسبه $m$ در هر تکرار است. این الگوریتم به جای میانگین $a$ و $b$ محل تقاطع خط واصل $(a,f(a)) $ و $(b,f(b))$ با محور $x$ به عنوان $m$ انتخاب میشود. از این بابت نیز رفتاری شبیه الگوریتم ریشهیابی نیوتن-رافسون دارد که در آنجا خط مماس به نمودار به جای خط واصل ابتدا و انتهای بازه استفاده میشود. قطعه کد زیر یک نمونه پیادهسازی الگوریتم ریشهیابی نابجایی است.
def falsePosition(f: "function", start: float, end: float, e: float, maxIteration : int):
it = 0
while True:
m = start - f(start) * ((end - start) / (f(end) - f(start)))
if end - start < e or f(m) == 0 or it == maxIteration:
break
if f(start) * f(m) < 0:
end = m
else:
start = m
it += 1
return m
الگوریتم ریشهیابی وتری
[برگرد بالا]
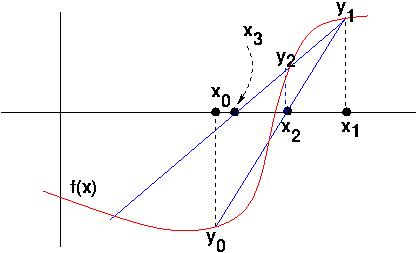
حالت دوم پیادهسازی الگوریتم نیوتن-رافسون این حسن را دارد که نیاز به محاسبه فرمولی مشتق و ارسال آن به تابع نداریم و به جای آن از یک تقریب استفاده میکنیم. الگوریتم ریشهیابی وتری (روش سکانت) نیز به همین ترتیب به جای استفاده از مشتق در خود نقطه، شیب خط واصل بین این نقطه و نقطه قبلی در دنباله را استفاده میکند. بنابراین یک نمونه کد پیادهسازی الگوریتم وتری با زبان برنامهنویسی پایتون به ترتیب زیر است.
def secant(f: "function", x0: float, x1: float, e: float, maxIteration : int):
it = 0
while True:
x2 = x1 - f(x1) * ((x0 - x1) / (f(x0) - f(x1)))
if abs(f(x2)) < e or it == maxIteration:
break
x0, x1= x1, x2
it += 1
return x2
نکته مهم این الگوریتم آن است که با این روش نقاط دنباله لزوما داخل بازه اولیه قرار نمیگیرند. بنابراین ممکن است ریشهای خارج از بازه یافت شود یا هرگز به ریشهای همگرا نشود. بنابراین انتخاب دو عدد ابتدایی نقش مهمی در عملکرد الگوریتم دارد و نکته جالبتر این است که لزومی ندارد تابع در این بازه اولیه ریشه داشته باشد! کافی است تابع secant را به صورت زیر فراخوانی کنید که دو عدد 4 و 10 در شروع الگوریتم ریشهیابی وتری استفاده شده و در نهایت عدد $\sqrt{2}$ با دقت مطلوبی محاسبه میشود!
secant(lambda x : x ** 2 - 2, 4, 10, 0.000001, 100)
الگوریتم ریشهیابی تکرار نقطه ثابت
[برگرد بالا]
الگوریتم ریشهیابی تکرار نقطه ثابت (روش تکرار ساده) که بر اساس قضیه نقطه ثابت ارائه شده، پیشنیازهای پیچیدهتری نسبت به روشهای قبل دارد. جهت استفاده از این الگوریتم برای حل معادله $f(x)=0$ در بازه $a$ تا $b$، باید شکل آن را به $g(x)=x$ تبدیل کرد به نحوی که $g(x)$ هم از این بازه خارج نبوده و قدر مطلق مشتقش در این بازه نیز کمتر از یک باشد.
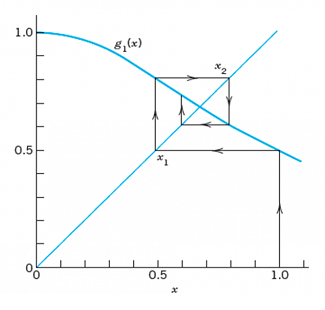
قطعه کد زیر یک نمونه پیادهسازی الگوریتم ریشهیابی تکرار نقطه ثابت با زبان برنامهنویسی پایتون است.
def fixedPoint(g: "function", x0: float, e: float, maxIteration : int):
it = 0
while True:
x1 = g(x0)
if abs(x1 - x0) < e or it == maxIteration:
break
x0 = x1
it += 1
return x1