الگوریتم فلوید-وارشال (Floyd-Warshall) یک الگوریتم مبتنی بر روش برنامهنویسی پویا برای محاسبه کوتاهترین مسیر بین هر دو جفت گره گرافهای وزندار است. دو الگوریتم رایج دایکسترا و بلمن-فورد روشهای محاسبه کوتاهترین مسیر از مبدأ ثابت هستند که در صورت تکرار آنها به ازای هر گره عملکردی همانند الگوریتم فلوید-وارشال دارند. اما این الگوریتم ویژگیهایی دارد که آن را برجسته میکند:
1) پیادهسازی سادهتری دارد.
2) بر خلاف الگوریتم دایکسترا برای گرافهایی شامل یال با وزن منفی نیز قابل استفاده است.
3) در حالت کلی مرتبه زمانی بهتری نسبت به الگوریتم بلمن-فورد دارد.
4) همانند الگوریتم بلمن-فورد قابلیت تشخیص دور منفی را دارد.
فرض کنید ماتریس مجاورت گراف را با $M_{ n \times n } $ و گرههای گراف را به صورت $\{ v_1, v_2, v_3, \cdots, v_n \} $ نمایش دهیم. اگر ماتریس $D^{(k)}_{n \times n}$ معرف ماتریس طول کوتاهترین مسیر بین گرههای گراف تنها با اجازه عبور از گرههای $\{v_1,v_2,v_3,\cdots,v_k\}$ باشد، ماتریس $D^{(n)}$ جواب مسئله خواهد بود. همچین $D^{(0)}$ همان $M$ است (چرا؟). پس محاسبه کوتاهترین مسیر بین گرهها به محاسبه ماتریس $D^{(n)}$ تبدیل میشود.
کوتاهترین مسیر از گره $v_i$ به گره $v_j$ با اجازه عبور از گره $v_1$ یا مسیر مستقیم بین آن دو (با اندازه $M_{ij}$) است یا مسیری که از گره $v_1$ (با اندازه $M_{i1}+M_{1j}$) میگذرد؛ یعنی:
\[D^{(1)}_{ij}= min\{ M_{ij}, M_{i1}+M_{1j} \} \]
با استفاده از این رابطه درایههای ماتریس $D^{(1)}$ از روی ماتریس مجاورت (یا همان ماتریس $D^{(0)}$) قابل محاسبه است. درایههای ماتریس $D^{(2)}$ طول کوتاهترین مسیرها با اجازه عبور از گرههای $v_1$ و $v_2$ است. چنین مسیرهایی یا بدون استفاده از گره $v_2$ هستند (یعنی همان $D^{(1)}_{ij}$) یا با عبور از این گره. اگر از این گره استفاده شود، طول کوتاهترین مسیر $D^{(1)}_{i2} + D^{(1)}_{2j} $ خواهد بود؛ چرا که $D^{(1)}_{i2}$ طول کوتاهترین مسیر از گره $v_i$ به این گره و $D^{(1)}_{2j} $ طول کوتاهترین مسیر از آن به گره $v_j$ است؛ پس:
\[D^{(2)}_{ij}= min\{ D^{(1)}_{ij}, D^{(1)}_{i2}+D^{(1)}_{2j} \} \]
این استدلال برای محاسبه هر کدام از ماتریسهای $D^{(k)}$ برقرار است و در حالت کلی میتوان نوشت:
\[D^{(k)}_{ij}= min\{ D^{(k-1)}_{ij}, D^{(k-1)}_{ik}+D^{(k-1)}_{kj} \} \; ; \qquad 0 < k \leq n \;, \; D^{(0)} = M \]
رابطه فوق مبنای کار الگوریتم فلوید-وارشال برای محاسبه طول کوتاهترین مسیر بین گرههای یک گراف است.
مسیریابی با استفاده از الگوریتم فلوید-وارشال
[برگرد بالا]
الگوریتم بحث شده تنها برای محاسبه اندازه کوتاهترین مسیر بین گرههای گراف بوده و امکان تشخیص گرههای این مسیر را ندارد. برای رفع این مشکل از ماتریس $ P_{n \times n}$ استفاده میشود که در ابتدا همه عناصر آن صفر است. طی محاسبات ماتریسهای $D^{(k)}$ اگر گره $k$ در کوتاهترین مسیر بین دو گره $i$ و $j$ انتخاب شد مقدار $k$ در $P_{ij}$ قرار داده میشود. به این ترتیب در انتهای الگوریتم یک شماره گره واسط بین دو گره $i$ و $j$ در درایه $P_{ij}$ موجود است. این درایه تنها در شرایطی صفر خواهد ماند که یا مسیری بین دو گره وجود نداشته، یا کوتاهترین مسیر یال مستقیم بین آن دو باشد. با مشخص شدن این گره واسط، تشخیص مسیر بهینه از مبدأ به مقصد تبدیل به تشخیص مسیر بهینه از مبدأ به این گره و از این گره به مقصد میگردد. تشخیص چنین مسیرهایی نیز از طریق همین ماتریس به صورت بازگشتی انجام میگیرد. به عنوان مثال برای گراف زیر:
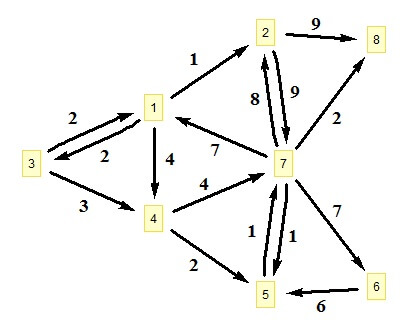
ماتریسهای مجاورت ($M$)، اندازه مسیرهای بهینه ($D$) و $P$ به این ترتیب است:
\[M = \begin{pmatrix} 0 & 1 & 2 & 4 & \infty & \infty & \infty & \infty \\ \infty & 0 & \infty & \infty & \infty & \infty & 9 & 9 \\ 2 & \infty & 0 & 3 & \infty & \infty & \infty & \infty \\ \infty & \infty & \infty & 0 & 2 & \infty & 4 & \infty \\ \infty & \infty & \infty & \infty & 0 & \infty & 1 & \infty \\ \infty & \infty & \infty & \infty & 6 & 0 & \infty & \infty \\ 7 & 8 & \infty & \infty & 1 & 7 & 0 & 2 \\ \infty & \infty & \infty & \infty & \infty & \infty & \infty & 0 \end{pmatrix}\]
\[D = \begin{pmatrix} 0 & 1 & 2 & 4 & 6 & 14 & 7 & 9 \\ 16 & 0 & 18 & 20 & 10 & 16 & 9 & 9 \\ 2 & 3 & 0 & 3 & 5 & 13 & 6 & 8 \\ 10 & 11 & 12 & 0 & 2 & 10 & 3 & 5 \\ 8 & 9 & 10 & 12 & 0 & 8 & 1 & 3 \\ 14 & 15 & 16 & 18 & 6 & 0 & 7 & 9 \\ 7 & 8 & 9 & 11 & 1 & 7 & 0 & 2 \\ \infty & \infty & \infty & \infty & \infty & \infty & \infty & 0 \end{pmatrix} \qquad P = \begin{pmatrix} 0 & 0 & 0 & 0 & 4 & 7 & 5 & 7 \\ 7 & 0 & 7 & 7 & 7 & 7 & 0 & 0 \\ 0 & 1 & 0 & 0 & 4 & 7 & 5 & 7 \\ 7 & 7 & 7 & 0 & 0 & 7 & 5 & 7 \\ 7 & 7 & 7 & 7 & 0 & 7 & 0 & 7 \\ 7 & 7 & 7 & 7 & 0 & 0 & 5 & 7 \\ 0 & 0 & 1 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \end{pmatrix}\]
بر اساس این اطلاعات، کوتاهترین مسیر از گره شماره 1 به گره شماره 7 به این ترتیب به دست میآید:
1) کوتاهترین مسیر از گره شماره 1 به گره شماره 7 از گره شماره 5 (درایه $P_{17}$) عبور میکند.
\[v_1 \rightarrow \cdots \rightarrow v_5 \rightarrow \cdots \rightarrow v_7 \]
2) کوتاهترین مسیر از گره شماره 5 به گره شماره 7 یال مستقیم آنها است (درایه $P_{57}$).
\[v_1 \rightarrow \cdots \rightarrow v_5 \rightarrow v_7 \]
3) کوتاهترین مسیر از گره شماره 1 به گره شماره 5 از گره شماره 4 (درایه $P_{15}$) عبور میکند.
\[v_1 \rightarrow \cdots \rightarrow v_4 \rightarrow \cdots \rightarrow v_5 \rightarrow v_7 \]
4) کوتاهترین مسیر از گره شماره 4 به گره شماره 5 یال مستقیم آنها است (درایه $P_{45}$).
\[v_1 \rightarrow \cdots \rightarrow v_4 \rightarrow v_5 \rightarrow v_7 \]
5) کوتاهترین مسیر از گره شماره 1 به گره شماره 4 یال مستقیم آنها است (درایه $P_{14}$).
\[v_1 \rightarrow v_4 \rightarrow v_5 \rightarrow v_7 \]
به این ترتیب مسیر بهینه با اندازه 7 (درایه $D_{17}$) مشخص شد.
\[v_1 \xrightarrow{4} v_4 \xrightarrow{2} v_5 \xrightarrow{1} v_7 \]
الگوریتم فلوید-وارشال برای هر گراف با وزنهای نامنفی همواره درست عمل میکند. اگر گراف وزن منفی نیز داشته ولی دور منفی نداشته باشد، باز هم عملکرد درستی خواهد داشت. به عنوان مثال، اگر در گراف فوق $M_{12} = -1$ بود، نتایج به این ترتیب میشد:
\[M = \begin{pmatrix} 0 & -1 & 2 & 4 & \infty & \infty & \infty & \infty \\ \infty & 0 & \infty & \infty & \infty & \infty & 9 & 9 \\ 2 & \infty & 0 & 3 & \infty & \infty & \infty & \infty \\ \infty & \infty & \infty & 0 & 2 & \infty & 4 & \infty \\ \infty & \infty & \infty & \infty & 0 & \infty & 1 & \infty \\ \infty & \infty & \infty & \infty & 6 & 0 & \infty & \infty \\ 7 & 8 & \infty & \infty & 1 & 7 & 0 & 2 \\ \infty & \infty & \infty & \infty & \infty & \infty & \infty & 0 \end{pmatrix}\]
\[D = \begin{pmatrix} 0 & -1 & 2 & 4 & 6 & 14 & 7 & 8 \\ 16 & 0 & 18 & 20 & 10 & 16 & 9 & 9 \\ 2 & 1 & 0 & 3 & 5 & 13 & 6 & 8 \\ 10 & 9 & 12 & 0 & 2 & 10 & 3 & 5 \\ 8 & 7 & 10 & 12 & 0 & 8 & 1 & 3 \\ 14 & 13 & 16 & 18 & 6 & 0 & 7 & 9 \\ 7 & 6 & 9 & 11 & 1 & 7 & 0 & 2 \\ \infty & \infty & \infty & \infty & \infty & \infty & \infty & 0 \end{pmatrix} \qquad P = \begin{pmatrix} 0 & 0 & 0 & 0 & 4 & 7 & 5 & 2 \\ 7 & 0 & 7 & 7 & 7 & 7 & 0 & 0 \\ 0 & 1 & 0 & 0 & 4 & 7 & 5 & 7 \\ 7 & 7 & 7 & 0 & 0 & 7 & 5 & 7 \\ 7 & 7 & 7 & 7 & 0 & 7 & 0 & 7 \\ 7 & 7 & 7 & 7 & 0 & 0 & 5 & 7 \\ 0 & 1 & 1 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \end{pmatrix}\]
اگر گراف دور منفی داشته باشد، الگوریتم خروجی درستی نخواهد داشت. به عنوان مثال، اگر در گراف فوق $M_{27} = -9$ بود، نتایج زیر حاصل میشد:
\[M = \begin{pmatrix} 0 & 1 & 2 & 4 & \infty & \infty & \infty & \infty \\ \infty & 0 & \infty & \infty & \infty & \infty & -9 & 9 \\ 2 & \infty & 0 & 3 & \infty & \infty & \infty & \infty \\ \infty & \infty & \infty & 0 & 2 & \infty & 4 & \infty \\ \infty & \infty & \infty & \infty & 0 & \infty & 1 & \infty \\ \infty & \infty & \infty & \infty & 6 & 0 & \infty & \infty \\ 7 & 8 & \infty & \infty & 1 & 7 & 0 & 2 \\ \infty & \infty & \infty & \infty & \infty & \infty & \infty & 0 \end{pmatrix}\]
\[D = \begin{pmatrix} -1 & 0 & 1 & 3 & -7 & -1 & -9 & -6 \\ -2 & -1 & 0 & 2 & -8 & -2 & -10 & -7 \\ 1 & 2 & 0 & 3 & -5 & 1 & -7 & -4 \\ 10 & 11 & 12 & 0 & 2 & 10 & 2 & 5 \\ 8 & 9 & 10 & 12 & 0 & 8 & 0 & 3 \\ 14 & 15 & 16 & 18 & 6 & 0 & 6 & 9 \\ 6 & 7 & 8 & 10 & 0 & 6 & -2 & 1 \\ \infty & \infty & \infty & \infty & \infty & \infty & \infty & 0 \end{pmatrix} \qquad P = \begin{pmatrix} 7 & 7 & 7 & 7 & 7 & 7 & 7 & 7 \\ 7 & 7 & 7 & 7 & 7 & 7 & 7 & 7 \\ 7 & 7 & 0 & 0 & 7 & 7 & 7 & 7 \\ 7 & 7 & 7 & 0 & 0 & 7 & 7 & 7 \\ 7 & 7 & 7 & 7 & 0 & 7 & 7 & 7 \\ 7 & 7 & 7 & 7 & 0 & 0 & 7 & 7 \\ 7 & 7 & 7 & 7 & 7 & 7 & 7 & 7 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \end{pmatrix}\]
تفاوت اصلی این خروجی با خروجی قبلی در اعداد منفی قطر اصلی ماتریس $D$ است. گرههایی که اعداد متناظر قطر اصلی آنها (در اینجا $ \{ v_1,v_2,v_7 \}$) منفی باشند، گرهی از یک مسیر با وزن منفی هستند. از این نکته برای تشخیص وجود دور منفی در گراف توسط الگوریتم فلوید-وارشال استفاده میشود.
تذکر: در گرافهای بدون جهت وجود یال منفی به معنی وجود دور منفی نیز هست (چرا؟).
پیادهسازی الگوریتم فلوید-وارشال
[برگرد بالا]
تابع Floyd_Warshall یک پیادهسازی ساده از الگوریتم فلوید-وارشال به زبان برنامهنویسی ++C است که با دریافت ماتریس مجاورت graph، اندازه کوتاهترین مسیر بین گرههای آن را در ماتریس D تولید میکند.
void Floyd_Warshal(int graph[MAX][MAX], int D[MAX][MAX], int P[MAX][MAX], int numberOfNodes){
for(int i = 0 ; i < numberOfNodes ; i++)
for(int j = 0 ; j < numberOfNodes ; j++){
D[i][j] = graph[i][j];
P[i][j] = -1;
}
for(int k = 0 ; k < numberOfNodes ; k++)
for(int i = 0 ; i < numberOfNodes ; i++)
for(int j = 0 ; j < numberOfNodes ; j++)
if(D[i][j] > D[i][k] + D[k][j]){
D[i][j] = D[i][k] + D[k][j];
P[i][j] = k;
}
}
در این پیادهسازی فرض بر آن است که وزن تمامی یالها نامنفی بوده و درایههای ستون اصلی ماتریس مجاورت صفر است (گراف حلقه ندارد یا حلقهها نادیده گرفته میشوند). همچنین فرض بر آن است که نبود یال بین دو گره با عدد بزرگی نابیشتر از نصف INT_MAX مشخص شده است.
تکرار حلقه بیرونی (با شمارنده k) ماتریسهای $D^{(k)}$ را تولید میکند. در ساخت ماتریس $ D^{(k)} $ از روی ماتریس $ D^{(k-1)} $ درایههای سطر و ستون $k$ بدون تغییر باقی مانده (چرا؟) و سایر درایهها نیز در صورت تغییر از همین درایهها ساخته میشوند. به این ترتیب نوشتن درایههای ماتریس جدید روی محل حافظه ماتریس قبلی اشکالی در محاسبات پیش نمیآورد. همچنین درایههای ماتریس P به جای صفر با $-1$ مقداردهی اولیه شده است (چرا؟).
در قطعه کد زیر الگوریتم فلوید-وارشال با استفاده از زبان برنامهنویسی Python پیادهسازی شده است.
def Floyd_Warshal(graph, D, P):
for i in range(len(graph)):
for j in range(len(graph)):
D[i][j] = graph[i][j]
P[i][j] = -1
for k in range(len(graph)):
for i in range(len(graph)):
for j in range(len(graph)):
if D[i][j] > D[i][k] + D[k][j]:
D[i][j] = D[i][k] + D[k][j]
P[i][j] = k
مرتبه زمانی الگوریتم فلوید-وارشال
[برگرد بالا]
بر اساس کد ارائه شده، پیادهسازی الگوریتم فلوید-وارشال از سه حلقه تکرار تو در تو تشکیل یافته است که هر کدام $n$ بار تکرار میشوند. بنابراین مرتبه زمانی اجرای این الگوریتم برای گرافی با $n$ گره $\theta (n^3) $ است.